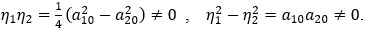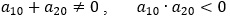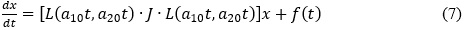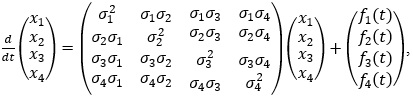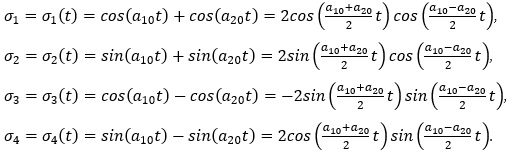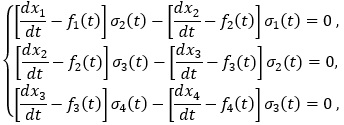В математичній теорії нелінійний багаточастотних коливань виникають системи диференціальних рівнянь вигляду 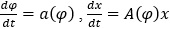 , які мають єдину функцію Гріна-Самойленка[1,2]. Такі системи називають регулярними. Дослідження регулярності деяких систем не завжди легко провести. В запропонованій доповіді розглядається питання регулярності системи диференціальних рівнянь
Записані змінні матриці 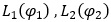 такі, що їх квадрат є постійною матрицею
а їх добуток є тотожно нульовою матрицею 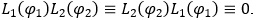
Звідси випливає, що квадрат суми цих матриць є постійною невиродженою матрицею: 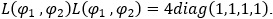 Це дає можливість записати обернену матрицю 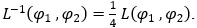
Якщо в системі (1) зробити заміну змінних 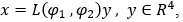 отримуємо нову систему вигляду
Має місце наступне твердження.
Теорема. Нехай виконуються одночасно дві нерівності
тоді при будь-якому значенні ε>0 системи (1) і (2) будуть регулярними.
При цьому знайдено додатно визначену квадратичну форму з постійними коефіцієнтами V, похідна якої вздовж розв’язків системи (2) є додатно визначеною. Ця квадратична форма має вигляд
де параметр p1- приймає достатньо великі додатні значення, а параметр p2 приймає два значення 2 або -2.
Зауваження. В теоремі першу нерівність (3) можна замінити протилежною 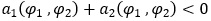 і тоді при виконанні другої нерівності 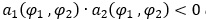 системи (2) і (1) будуть регулярними.
Розглядаючи частинний випадок системи (1), припускаємо, що функції 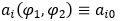 є постійними. Отримуємо систему
яка буде регулярною при одночасному виконанні двох нерівностей:
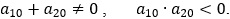 В системі (4) розв’язки перших двох рівнянь 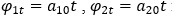 підставимо в третє. Отримаємо нестаціонарну систему, яка складається з чотирьох рівнянь:
Оскільки система (4) при виконанні відповідних нерівностей є регулярною, то лінійна система (5) при цих же умовах є гіперболічною на всій осі R.
В цьому можна переконатись провівши в системі (5) заміну змінних Ляпунова 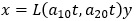 . Після цієї заміни система (5) переходить в систему з постійними коефіцієнтами
де 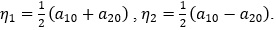 Характеристичне рівняння для системи (6) має вигляд: 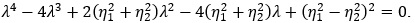
Записане рівняння не має нульових і чисто уявних розв’язків 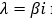 при виконанні двох умов: 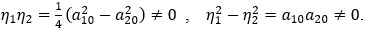
Таким чином, при виконанні нерівностей 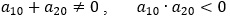 неоднорідна система неоднорідна система
матиме єдиний обмежений на всій осі R розв’язок x=x* (t)=(x1* (t),…,x4* (t)) при кожній фіксованій неперервній і обмеженій на R вектор-функції f(t)=(f1 (t),…,f4 (t)) . Систему (7) записуємо у вигляді
де позначено
З вигляду записаної вище системи випливає, що система
матиме обмежений на всій осі R розв’язок x=x* (t)=(x1* (t),…,x4* (t)) при кожній фіксованій неперервній і обмеженій на R вектор-функції f(t)=(f1 (t),…,f4 (t)). Але можливо цей обмежений розв’язок не єдиний.
Список літератури:
1. V.L. Kulyk, N.V. Stepanenko "Green-Samoilenko function of linear extensions of dynamical systems on a torus". Journal of mathematical sciences. Vol.263. No2. May 2022. P.238-247
2. В. Л. Кулик, Г. М. Кулик, Н. В. Степаненко "Про деякі конструкції регулярних лінійних розширень динамічних ситем на торі". ISSN 1562-3076. Нелiнiйнi коливання, 2023, т. 26, No 1 . С. 77-94
|








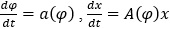 , які мають єдину функцію Гріна-Самойленка[1,2]. Такі системи називають регулярними. Дослідження регулярності деяких систем не завжди легко провести. В запропонованій доповіді розглядається питання регулярності системи диференціальних рівнянь
, які мають єдину функцію Гріна-Самойленка[1,2]. Такі системи називають регулярними. Дослідження регулярності деяких систем не завжди легко провести. В запропонованій доповіді розглядається питання регулярності системи диференціальних рівнянь 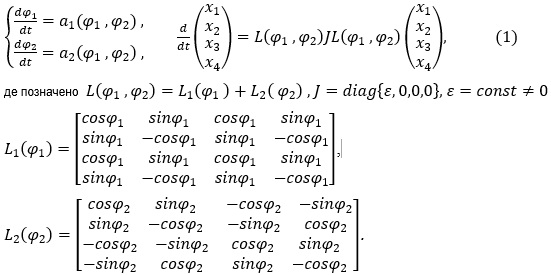
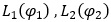 такі, що їх квадрат є постійною матрицею
такі, що їх квадрат є постійною матрицею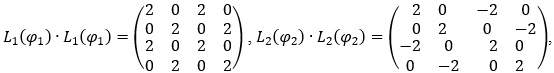
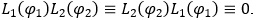
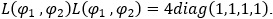 Це дає можливість записати обернену матрицю
Це дає можливість записати обернену матрицю 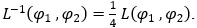
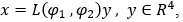 отримуємо нову систему вигляду
отримуємо нову систему вигляду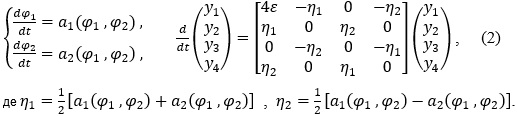
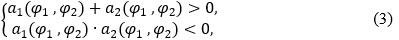
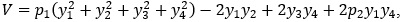
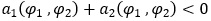 і тоді при виконанні другої нерівності
і тоді при виконанні другої нерівності 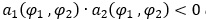 системи (2) і (1) будуть регулярними.
системи (2) і (1) будуть регулярними.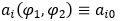 є постійними. Отримуємо систему
є постійними. Отримуємо систему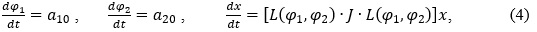
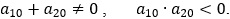 В системі (4) розв’язки перших двох рівнянь
В системі (4) розв’язки перших двох рівнянь 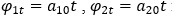 підставимо в третє. Отримаємо нестаціонарну систему, яка складається з чотирьох рівнянь:
підставимо в третє. Отримаємо нестаціонарну систему, яка складається з чотирьох рівнянь: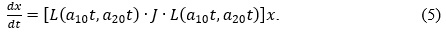
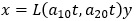 . Після цієї заміни система (5) переходить в систему з постійними коефіцієнтами
. Після цієї заміни система (5) переходить в систему з постійними коефіцієнтами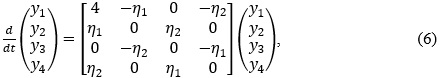
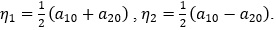 Характеристичне рівняння для системи (6) має вигляд:
Характеристичне рівняння для системи (6) має вигляд: 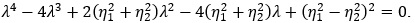
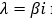 при виконанні двох умов:
при виконанні двох умов: