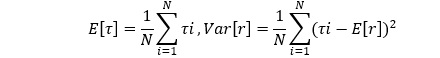Затримки в доставці БПЛА можуть виникати з різних причин: зміни погоди, перевантаження зон, обмеження маршруту або несподівані події в повітряному просторі. Для точного моделювання таких затримок доцільно використовувати стохастичний підхід, що дозволяє враховувати випадковість і невизначеність у поведінці системи. Найбільш доцільним методом у даному контексті є метод Монте-Карло, який забезпечує генерацію великої кількості сценаріїв на основі розподілу ймовірностей [1].
Стохастична модель затримки
Вводиться змінна затримки τ, яка для кожного дрона моделюється як випадкова величина, що підпорядковується експоненційному розподілу:
де λ — параметр інтенсивності (середня частота появи перешкод), який задається відповідно до реальних умов (наприклад, погодна статистика, щільність зон, частота перенаправлень) [2].
Процедура симуляції
Метод Монте-Карло полягає в багаторазовому прогоні симуляції з випадковими значеннями затримок τi, що дозволяє оцінити вплив непередбачуваних факторів на середній час доставки, MAE [3] та частоту перенаправлень:
- На кожному кроці для кожного БПЛА додається випадкова затримка τi∼Exp(λ).
- Після N симуляцій обчислюються середні показники:
де τi — значення затримки у i-ій симуляції; E[τ] — математичне сподівання (середнє значення) затримок за результатами симуляцій. Показує типовий час затримки; Var[τ] — дисперсія, яка вимірює розкид затримок відносно середнього. Чим вона вища, тим менш передбачувані затримки [3].
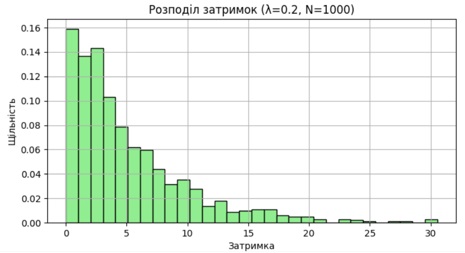
На рисунку 1 представлено приклад розподілу затримок для 1000 дронів, згенерованих методом Монте-Карло при параметрі λ=0.2:
Рисунок 1 – Гістограма розподілу затримок (метод Монте-Карло)
Як видно, більшість затримок є короткими (0–5 од.), а великі затримки трапляються рідко — характерно для експоненційного розподілу.
На рисунка 2 та 3 наведено графіки, які демонструють вплив параметрів симуляціі на розподіл затримок.
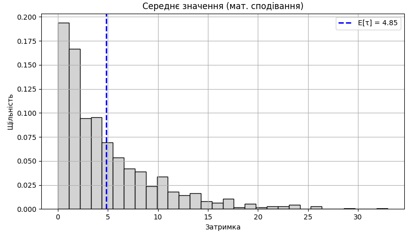
Риснок 2 - Середнє значення математичного сподівання (E[τ])
Цей графік демонструє розподіл затримок, аналогічний попередньому, але з додатковою вертикальною синьою пунктирною лінією, що позначає середнє значення затримок: E[τ] ≈ 4.85 – це середнє арифметичне всіх згенерованих затримок. Його положення відображає, як зміщується центр маси розподілу праворуч у разі високої дисперсії.
Рисунок 3 – Дисперсія (Var[τ]) розкиду навколого середнього значення математичного сподівання
Цей графік доповнює попередній двома червоними пунктирними лініями:
- Вони показують +σ та -σ відносно E[τ], тобто стандартне відхилення (σ ≈ 4.92).
- Це дає змогу оцінити, наскільки дані відхиляються від середнього (68% значень для експоненційного розподілу мають знаходитись у межах [E[τ] ± σ]).
Запропонована стохастична модель затримок на основі методу Монте-Карло дозволяє гнучко моделювати вплив випадкових перешкод на час доставки БПЛА в міських умовах. Завдяки використанню експоненційного розподілу, система отримує можливість враховувати різні інтенсивності появи подій та їхнє статистичне відображення в розподілі затримок.
Побудовані графіки демонструють не лише характер розподілу, а й поведінку середнього значення та дисперсії, що є ключовими метриками для оцінювання стабільності й надійності маршрутів.
Отримані результати формують основу для адаптивного реагування системи управління, що розглядається у наступному підрозділі.
Список літератури
1. Єна, М. (2025). СИМУЛЯЦІЯ ТРАФІКУ БПЛА В МІСЬКИХ ПОВІТРЯНИХ МЕРЕЖАХ ЗА МОДЕЛЯМИ МОНТЕ-КАРЛО ТА ДИСКРЕТНО-ПОДІЙНОГО МОДЕЛЮВАННЯ. Випробування та сертифікація, (1(7), 115-122. https://doi.org/10.37701/ts.07.2025.13
2. Ghayouraneh, S., Rankin, J. Monte Carlo Simulations to Predict Traffic Flow Patterns of UAM Vehicles. University of Arkansas at Fayetteville, South Dakota School of Mines and Technology, November 2020. [Online]. URL: https://scholarworks.uark.edu/etd/4136.
3. Chow, J. Y. J. Dynamic UAV-based traffic monitoring under uncertainty as a stochastic arc-inventory routing policy. International Journal of Transportation Science & Technology, 2016, vol. 5, no. 3, pp. 167-185. https://doi.org/10.1016/j.ijtst.2016.11.002.
|
Голосування 
Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License
Знайшли помилку? Виділіть помилковий текст мишкою і натисніть Ctrl + Enter