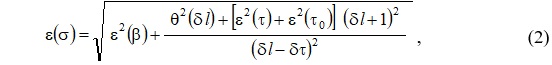Контроль механічних напружень в елементах конструкцій є актуальною проблемою для космічної та авіаційної техніки, хімічної промисловості, атомної енергетики. Перспективним шляхом подолання цієї проблеми є впровадження акустичної тензометрії – сукупності методів контролю напружень, що базуються на вимірюванні характеристик пружних хвиль, які поширюються в досліджуваній деталі.
Обмежуючись розглядом однорідної одновісної деформації первісно ізотропного середовища [1], можна записати основне розрахункове співвідношення акустопружності після лінеаризації у вигляді:
де σ – шукані компоненти тензора напружень; 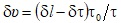 – відповідні компоненти матриці значень відносної зміни швидкості ультразвуку; β – відповідні компоненти матриці акустопружних коефіцієнтів.
Визначення внутрішніх напружень σ за зміною часу τ поширення ультразвукової хвилі в зразку є типовим прикладом непрямих вимірювань. Відносна похибка напруження визначається співвідношенням:
де θ(δl) – абсолютна похибка прямого вимірювання відносної продольної деформації δl зразка; ε(...)– відносна похибка прямого вимірювання деякого параметру. Якщо систематичні похибки виключені, а діапазон зміни кожного параметра в формулі (2) визначається лише можливостями серійної вимірювальної апаратури, то ε(σ) може набувати значень від 0,0012 до 73,50.
При фіксованих значеннях похибки акустопружного коефіцієнту ε(β) функція залежності відносної похибки напруження ε(σ) від похибки вимірювання часу ε(τ) та її перша похідна монотонно зростають. Якщо поставлена задача мінімізації ε(σ) при фіксованих значеннях ε(β), ǀδl-δτǀ та θ(δl), легко зазначити границю, до якої доцільно зменшувати ε(τ). Також очевидно, що знаючи коефіцієнт β з малою похибкою, але вимірюючи час поширення τ з недостатньою точністю, експериментатор отримає великі значення ε(σ).
Найбільш істотно на значення ε(σ) впливають знаменник дробу ǀδl-δτǀ та похибка визначення коефіцієнту ε(β), причому зменшення параметра ǀδl-δτǀ при незмінності інших параметрів суттєво збільшує значення функції. Навіть якщо припустити, що відомим є точне значення β, а вимірювання δl та τ виконані з вельми малою відносною похибкою (наприклад, 1·10‒5), то виявиться, що ε(σ) «укладається» в 10-відсоткові границі лише тоді, коли ǀδl-δτǀ перевищує деяке порогове значення. Якщо дозволений рівень ε(σ) задається заздалегідь, то збільшення значення ǀδl-δτǀ може істотно пом'якшити вимоги до точності вимірювання τ. Наприклад, якщо при акустичному діагностуванні розтяжного напруження в двох конгруентних циліндричних зразках зі сталі та алюмінію припустити, що для обох матеріалів акустопружний коефіцієнт визначений з однаковою похибкою ε(β)=0,079, то виявиться, що рівень ε(σ)˂=0,100 може бути забезпечений при вимірюванні часу поширення з відносною похибкою: в алюмінії – не вище за 6·10–5; в сталі – не вище за 2·10–5. Враховуючи, що ǀδl-δτǀ визначається, в основному, властивостями матеріалу зразка та навантаженням, можна сформулювати такі висновки:
1) при незмінній точності вимірювання часу τ точніші результати визначення напружень досягаються при сильнішому навантаженні зразка;
2) якщо декілька зразків однакової геометрії з різних матеріалів піддані однаковому навантаженню, то похибка вимірювання напруження в кожному з них буде індивідуальною, навіть при вимірюванні τ в усіх зразках з однаковою відносною похибкою.
Окремим параметром, що істотно впливає на рівень ε(σ), є похибка акустопружного коефіцієнту. Цей коефіцієнт може бути визначений як експериментально, так і розрахунковим шляхом, через пружні модулі другого та третього порядку [2]. Розрахунковий шлях виглядає, на перший погляд, переважним. Однак для досліджених конструкційних матеріалів похибка вимірювання опублікованих значень модулів пружності третього порядку сягає іноді сотень відсотків. Тому на даному етапі використання розрахункових значень акустопружних коефіцієнтів не забезпечує задовільної точності визначення напружень і не може бути рекомендоване для практичного застосування. Більш перспективним виглядає експериментальний підхід до визначення акустопружних коефіцієнтів.
Список літератури
1. Анисимов В. О. Лінеаризація основних рівнянь акустодіагностики напружень. XXXІV Міжнародна науково-практична конференція «World Trends in the Development of Scientific Progress»: collection of abstracts (August 14-16, 2024) Varna, Bulgaria. International Scientific Unity, 2024. ‒ С. 178-180.
2. Анисимов В. О. Акустопружні коефіцієнти конструкційних матеріалів та похибки їх визначення / Анисимов В. О., Дюбченко М. Є., Ковальов Ю. В., Корнєва Н. М. // Collection of Scientific Papers with Proceedings of the 1st International Scientific and Practical Conference «Modern Science, Economy and Digital Innovation», January 29-31, 2025. Bucharest, Romania.‒ P. 185-188.
|









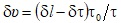 – відповідні компоненти матриці значень відносної зміни швидкості ультразвуку; β – відповідні компоненти матриці акустопружних коефіцієнтів.
– відповідні компоненти матриці значень відносної зміни швидкості ультразвуку; β – відповідні компоненти матриці акустопружних коефіцієнтів.