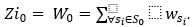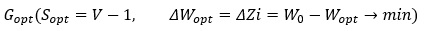Процес розвитку прикладних комп'ютерних систем описано в монографії [1]. Системний аналіз процесу комп'ютеризації показав, що в даний час мова йде про створення соціо-кібер-фізичних систем (СКФС).
Вони характеризуються зростаючою структурною складністю інформаційних процесів взаємодії підсистем. Для таких систем можна розглядати два рівні структурної оптимізації: транспортний рівень комунікацій на підприємстві та інформаційний рівень процесів функціонування систем. Для першого класу структур відомі методи побудови мінімальних остових дерев за критерієм мінімізації сумарної довжини комунікацій [2].
Для інформаційних структур актуальною є задача інформаційної логістики, коли необхідно зменшити інформаційну структуру до рівня мінімального остового дерева шляхом видалення та перенаправлення малорозмірних інформаційних потоків по інших коротких зв'язках.
Постановка задачі: У цьому разі задача оптимізації представляється таким чином: для неорієнтованого графа з дуплексними зв'язками:
Маємо вихідний граф G 0 (N,V,S 0,P 0,W 0 ), де V- множина вузлів, S 0- множина зав’язків у графі S 0≫V, P 0-множина шляхів у графі {p ijk (v i,v j )}-це один з можливих шляхів k між вузлами v i,v j. Кожен шлях складається з послідовності (ланцюжка) зв’язків p ijk=s i,s (i+1),…,s j, складність (довжину) шляху k будемо оцінювати кількістю ланцюгів n у шляху k , L(p ijk )=n(s i,s (i+1),...,s j,). W 0 – сумарний інформаційний потік в початковому графі, або його інформаційна завантаженість, далі «Zi», що рахується як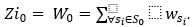 
Таким чином задачу оптимізації інформаційних структур підвищеної складності для СКФС можна сформулювати так:
Знайти оптимальну інформаційну структуру – неорієнтований остовий граф, без непродуктивних зв'язків зі збереженням доступу до всіх вузлів графа і перерозподілом їхніх потоків за іншими короткими маршрутами. При цьому необхідно, щоб збільшення його інформаційної завантаженості було мінімальним (Zi - min)
Евристичний метод побудови раціональної структури інфокомунікацій
Розглянемо сутність пропонованого методу у вигляді послідовності кроків макроалгоритму.
Крок 1. Підготовка всіх необхідних даних опису вихідного графа G0 (N,V,S0,P0,W0 ).
Крок 2. Визначаємо показник Zi графа (обчислюємо ΔZi на наступних ітераціях) ;
Крок 3. Формуємо впорядковану послідовність усіх зв'язків S≫V у порядку зростання їхньої пропускної здатності;
Крок 4. Знаходимо всі шляхи між парами вершин графа vi,vj. Упорядковуємо їх за зростанням їхньої довжини, або кількості ланок у ланцюжку шляху (si,si+1,...,sj,);
Крок 5. Вибираємо елемент на видалення у списку зв'язків. Вибираємо для нього один маршрут в області найкоротших шляхів. Інформаційний потік зв'язку, що видаляється, додаємо до всіх ланок зв'язків в обраному маршруті.
Крок 6. Оновлюємо масиви зв'язків і маршрутів.
Крок 7. Якщо кількість зв'язків S у графі не дорівнює V-1, то переходимо до кроку 2, інакше - крок 8.
Крок 8. Виведення результатів роботи методу: Zi, структура графа, склад потоків у кожному зв'язку кожного маршруту.
Приклад опису графів та їх перетворень
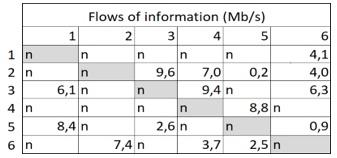
На рисунку 1 подано табличний опис вихідного графа. У прикладі обрано для ілюстрації просту структуру з шести підсистем.
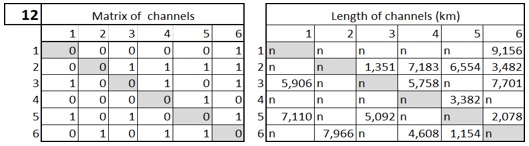
На рисунку 2 - графічне представлення вихідного графа. Для формування оптимальної структури комунікацій на підприємстві побудовано мінімальне остове дерево комунікації (рис. 3). Це передбачувана технічна структура каналів взаємодії між підсистемами.
Рис. 1 - Табличний опис вихідного графа
Результат: отримано мінімальне остове дерево комунікацій між підсистемами на підприємстві. Існуюча система (рис. 2) має сумарну довжину всіх каналів 68.437 км, у запропонованій схемі (рис. 3) вона складає 16.501 км. У підсумку економія кабелю для комунікацій становить 51.936 км. Це без урахування інфокомунікацій.
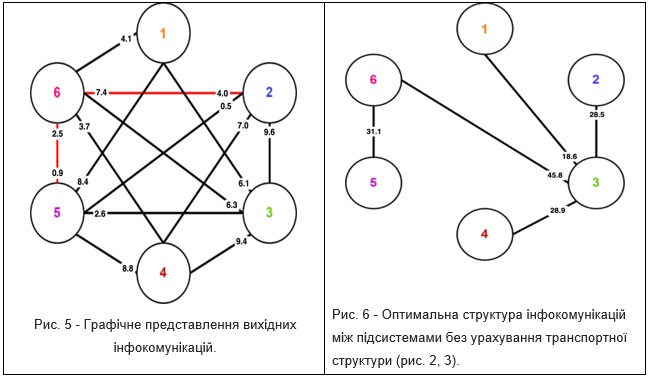
Для початкової структури комунікацій на підприємстві визначено інформаційні потоки в кожному її каналі. Вони описані у відповідній таблиці на рис 4. Її графічне представлення наведено на рис. 5. Результат побудови оптимальної структури інфокомунікацій з використанням описаного алгоритму наведено на рис. 6.
Рис. 4 - Табличний опис інформаційних потоків у вихідному графі.
У результаті використання зазначеного алгоритму було отримано мінімальне остове дерево графа інфокомунікацій з мінімальним збільшенням інформаційної завантаженості системи. Результатом оптимізації схеми інформаційних потоків між об’єктами є зменшення числа непродуктивних інфоканалів при сумарному навантаження у решти підсистем зросло з 81.3 Мб/с до 152.9 Мб/с, тобто на 71.6 Мб/с.
Висновки. Процес формування транспортної структури комунікацій та інфокомунікацій часто не збігається на підприємстві. Необхідно розв'язати задачу отримання узагальненої транспортно-інформаційної структури, однак вона потребує окремого розгляду.
У даній статті обрано найпростіший спосіб вибору альтернативних шляхів для інформаційних потоків за критерієм мінімальної кількості ланок у маршруті, що обирається. Навіть у цьому випадку час розв'язання задачі для складних систем досить великий.
У принципі під час вибору альтернативного шляху необхідно враховувати експлуатаційні характеристики його ланок: граничну пропускну спроможність ланок шляху, показники надійності маршрутів, вартості їхньої експлуатації та інші.
Для розширеної постановки завдання необхідно використовувати методи штучного інтелекту.
Перелік посилань:
1. Kosolapov A.A., Yehorov О. Y., Parpalita О.M. Synergy of systems - socio- cyber-physical systems (SCPS) Monographic series «European Science» Book 33. Part 1. In internationalen wissenschaftlich-geometrischen Datenbanken enthalten Included in International scientometric databases МONOGRAPHIE MONOGRAPHScientificWorld-NetAkhatAV Karlsruhe 2024.
2. Христофідес Н. Теорія графів: алгоритмічний підхід / Н. Христофідес ; пер. з англ. — Львів : Світ, 1978. — 432 с.
_______________________
Науковий керівник: Косолапов Анатолій Аркадійович, доктор технічних наук, професор
|
Голосування 
Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License
Знайшли помилку? Виділіть помилковий текст мишкою і натисніть Ctrl + Enter